|
RATE CONSTANTS AND THE ARRHENIUS EQUATION
This page looks at the way that rate constants vary with temperature and activation energy as shown by the Arrhenius equation. | |
|
Note: If you aren't sure what a rate constant is, you should read the page about orders of reaction before you go on. This present page is at the hard end of the rates of reaction work on this site. If you aren't reasonably confident about the basic rates of reaction work, explore the rates of reaction menu first. | |
|
The Arrhenius equation
Rate constants and rate equations You will remember that the rate equation for a reaction between two substances A and B looks like this: 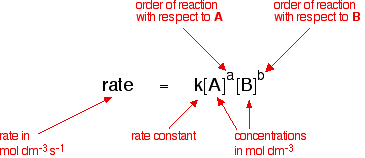 | |
|
Note: If you don't remember this, you must read the page about orders of reaction before you go on. Use the BACK button on your browser to return to this page. | |
|
The rate equation shows the effect of changing the concentrations of
the reactants on the rate of the reaction. What about all the other
things (like temperature and catalysts, for example) which also change
rates of reaction? Where do these fit into this equation? These are all included in the so-called rate constant - which is only actually constant if all you are changing is the concentration of the reactants. If you change the temperature or the catalyst, for example, the rate constant changes. This is shown mathematically in the Arrhenius equation. The Arrhenius equation  Starting with the easy ones . . .
| |
|
Note: If you aren't sure about activation energy, you should read the introductory page on rates of reaction before you go on. Use the BACK button on your browser to return to this page. | |
And then the rather trickier ones . . .
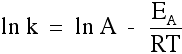 Using the Arrhenius equation The effect of a change of temperature You can use the Arrhenius equation to show the effect of a change of temperature on the rate constant - and therefore on the rate of the reaction. If the rate constant doubles, for example, so also will the rate of the reaction. Look back at the rate equation at the top of this page if you aren't sure why that is. What happens if you increase the temperature by 10°C from, say, 20°C to 30°C (293 K to 303 K)? The frequency factor, A, in the equation is approximately constant for such a small temperature change. We need to look at how e-(EA / RT) changes - the fraction of molecules with energies equal to or in excess of the activation energy. Let's assume an activation energy of 50 kJ mol-1. In the equation, we have to write that as 50000 J mol-1. The value of the gas constant, R, is 8.31 J K-1 mol-1. At 20°C (293 K) the value of the fraction is: 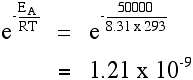 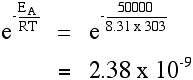 | |
|
Note: This approximation (about the rate of a reaction doubling for a 10 degree rise in temperature) only works for reactions with activation energies of about 50 kJ mol-1 fairly close to room temperature. If you can be bothered, use the equation to find out what happens if you increase the temperature from, say 1000 K to 1010 K. Work out the expression -(EA / RT) and then use the ex button on your calculator to finish the job. The rate constant goes on increasing as the temperature goes up, but the rate of increase falls off quite rapidly at higher temperatures. | |
|
The effect of a catalyst A catalyst will provide a route for the reaction with a lower activation energy. Suppose in the presence of a catalyst that the activation energy falls to 25 kJ mol-1. Redoing the calculation at 293 K: 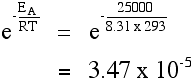 It's no wonder catalysts speed up reactions! Other calculations involving the Arrhenius equation If you have values for the rate of reaction or for the rate constant at different temperatures, you can use these to work out the activation energy of the reaction. Only one UK A' level Exam Board expects you to be able to do these calculations. They are included in my chemistry calculations book, and I can't repeat the material on this site. | |
Tuesday, 24 September 2013
RATE CONSTANTS AND THE ARRHENIUS EQUATION
Subscribe to:
Post Comments (Atom)
No comments:
Post a Comment