The structure of solids can be described as if they were
three-dimensional analogs of a piece of wallpaper. Wallpaper has
a regular repeating design that extends from one edge to the
other. Crystals have a similar repeating design, but in this case
the design extends in three dimensions from one edge of the solid
to the other.
We can unambiguously describe a piece of wallpaper by specifying the size, shape, and contents of the simplest repeating unit in the design. We can describe a three-dimensional crystal by specifying the size, shape, and contents of the simplest repeating unit and the way these repeating units stack to form the crystal.
The simplest repeating unit in a crystal is called a unit cell. Each unit cell is defined in terms of lattice points
the
points in space about which the particles are free to vibrate in
a crystal.
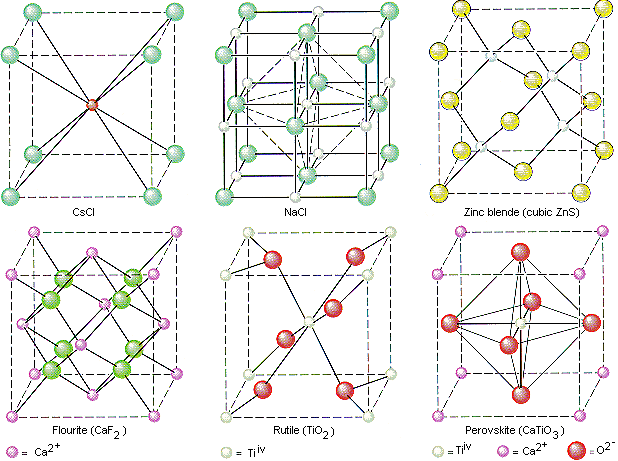
The structures of the unit cell for a variety of salts are shown below.
In 1850, Auguste Bravais showed that crystals could be divided
into 14 unit cells, which meet the following criteria.
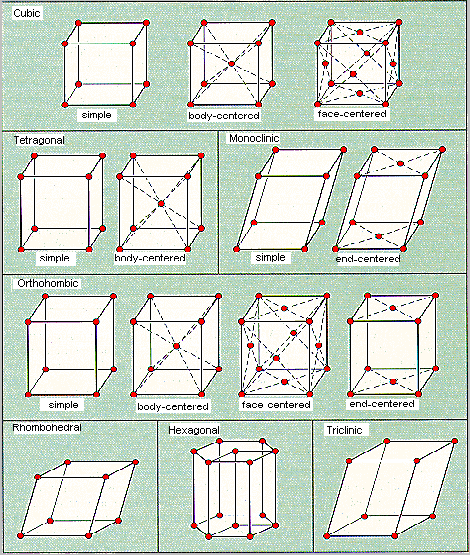These unit cells fall into seven categories, which differ in
the three unit-cell edge lengths (a, b, and c)
and three internal angles (a, � and g), as shown in the table
below.
We will focus on the cubic category, which includes the three
types of unit cellssimple
cubic, body-centered cubic, and face-centered cubicshown
in the figure below.
These unit cells are important for two reasons. First, a
number of metals, ionic solids, and intermetallic compounds
crystallize in cubic unit cells. Second, it is relatively easy to
do calculations with these unit cells because the cell-edge
lengths are all the same and the cell angles are all 90.
The simple cubic unit cell is the simplest repeating unit in a simple cubic structure. Each corner of the unit cell is defined by a lattice point at which an atom, ion, or molecule can be found in the crystal. By convention, the edge of a unit cell always connects equivalent points. Each of the eight corners of the unit cell therefore must contain an identical particle. Other particles can be present on the edges or faces of the unit cell, or within the body of the unit cell. But the minimum that must be present for the unit cell to be classified as simple cubic is eight equivalent particles on the eight corners.
The body-centered cubic unit cell is the simplest repeating unit in a body-centered cubic structure. Once again, there are eight identical particles on the eight corners of the unit cell. However, this time there is a ninth identical particle in the center of the body of the unit cell.
The face-centered cubic unit cell also starts with identical particles on the eight corners of the cube. But this structure also contains the same particles in the centers of the six faces of the unit cell, for a total of 14 identical lattice points.
The face-centered cubic unit cell is the simplest repeating unit in a cubic closest-packed structure. In fact, the presence of face-centered cubic unit cells in this structure explains why the structure is known as cubic closest-packed.
The lattice points in a cubic unit cell can be described in terms of a three-dimensional graph. Because all three cell-edge lengths are the same in a cubic unit cell, it doesn't matter what orientation is used for the a, b, and c axes. For the sake of argument, we'll define the a axis as the vertical axis of our coordinate system, as shown in the figure below.
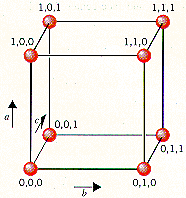The b axis will then describe movement across the front
of the unit cell, and the c axis will represent movement
toward the back of the unit cell. Furthermore, we'll arbitrarily
define the bottom left corner of the unit cell as the origin
(0,0,0). The coordinates 1,0,0 indicate a lattice point that is
one cell-edge length away from the origin along the a
axis. Similarly, 0,1,0 and 0,0,1 represent lattice points that
are displaced by one cell-edge length from the origin along the b
and c axes, respectively.
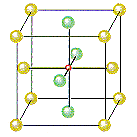
Thinking about the unit cell as a three-dimensional graph allows us to describe the structure of a crystal with a remarkably small amount of information. We can specify the structure of cesium chloride, for example, with only four pieces of information.
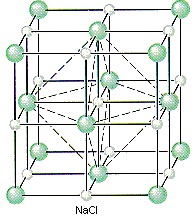
NaCl should crystallize in a cubic closest-packed array of Cl- ions with Na+ ions in the octahedral holes between planes of Cl- ions. We can translate this information into a unit-cell model for NaCl by remembering that the face-centered cubic unit cell is the simplest repeating unit in a cubic closest-packed structure.
There are four unique positions in a face-centered cubic unit cell. These positions are defined by the coordinates: 0,0,0; 0,1/2,1/2; 1/2,0,1/2; and 1/2,1/2,0. The presence of an particle at one corner of the unit cell (0,0,0) requires the presence of an equivalent particle on each of the eight corners of the unit cell. Because the unit-cell edge connects equivalent points, the presence of a particle in the center of the bottom face (0,1/2,1/2) implies the presence of an equivalent particle in the center of the top face (1,1/2,1/2). Similarly, the presence of particles in the center of the 1/2,0,1/2 and 1/2,1/2,0 faces of the unit cell implies equivalent particles in the centers of the 1/2,1,1/2 and 1/2,1/2,1 faces.
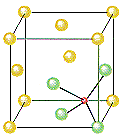
The figure below shows that there is an octahedral hole in the center of a face-centered cubic unit cell, at the coordinates 1/2,1/2,1/2. Any particle at this point touches the particles in the centers of the six faces of the unit cell.
The other octahedral holes in a face-centered cubic unit cell
are on the edges of the cell, as shown in the figure below.
We can therefore describe the structure of NaCl in terms of
the following information.
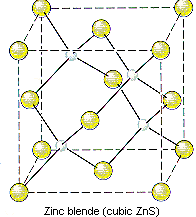
ZnS crystallizes as cubic closest-packed array of S2- ions with Zn2+ ions in tetrahedral holes. The S2- ions in this crystal occupy the same positions as the Cl- ions in NaCl. The only difference between these crystals is the location of the positive ions. The figure below shows that the tetrahedral holes in a face-centered cubic unit cell are in the corners of the unit cell, at coordinates such as 1/4,1/4,1/4. An atom with these coordinates would touch the atom at this corner as well as the atoms in the centers of the three faces that form this corner. Although it is difficult to see without a three-dimensional model, the four atoms that surround this hole are arranged toward the corners of a tetrahedron.
Because the corners of a cubic unit cell are identical, there
must be a tetrahedral hole in each of the eight corners of the
face-centered cubic unit cell. If S2- ions occupy the
lattice points of a face-centered cubic unit cell and Zn2+
ions are packed into every other tetrahedral hole, we get the
unit cell of ZnS shown in the figure below.
The structure of ZnS can therefore be described as follows.
Read more at:
We can unambiguously describe a piece of wallpaper by specifying the size, shape, and contents of the simplest repeating unit in the design. We can describe a three-dimensional crystal by specifying the size, shape, and contents of the simplest repeating unit and the way these repeating units stack to form the crystal.
The simplest repeating unit in a crystal is called a unit cell. Each unit cell is defined in terms of lattice points
the
points in space about which the particles are free to vibrate in
a crystal. The structures of the unit cell for a variety of salts are shown below.
- The unit cell is the simplest repeating unit in the crystal.
- Opposite faces of a unit cell are parallel.
- The edge of the unit cell connects equivalent points.
The Seven Categories of Bravais Unit Cells
| Category | Edge Lengths | Internal Angles | ||
| Cubic | (a = b = c) | (a = �/i> = g = 90o) | ||
| Tetragonal | (a = b 
c) |
(a = �/i> = g = 90o) | ||
| Monoclinic | (a
b
c) |
(a = �/i> = 90o
g) |
||
| Orthorhombic | (a
b
c) |
(a = �/i> = g = 90o) | ||
| Rhombohedral | (a = b = c) | (a = �/i> = g
90o) |
||
| Hexagonal | (a = b
c) |
(a = �/i> = 90o, g = 120o) | ||
| Triclinic | (a
b
c) |
(a
�/i>
g
90o) |
simple
cubic, body-centered cubic, and face-centered cubicshown
in the figure below. The simple cubic unit cell is the simplest repeating unit in a simple cubic structure. Each corner of the unit cell is defined by a lattice point at which an atom, ion, or molecule can be found in the crystal. By convention, the edge of a unit cell always connects equivalent points. Each of the eight corners of the unit cell therefore must contain an identical particle. Other particles can be present on the edges or faces of the unit cell, or within the body of the unit cell. But the minimum that must be present for the unit cell to be classified as simple cubic is eight equivalent particles on the eight corners.
The body-centered cubic unit cell is the simplest repeating unit in a body-centered cubic structure. Once again, there are eight identical particles on the eight corners of the unit cell. However, this time there is a ninth identical particle in the center of the body of the unit cell.
The face-centered cubic unit cell also starts with identical particles on the eight corners of the cube. But this structure also contains the same particles in the centers of the six faces of the unit cell, for a total of 14 identical lattice points.
The face-centered cubic unit cell is the simplest repeating unit in a cubic closest-packed structure. In fact, the presence of face-centered cubic unit cells in this structure explains why the structure is known as cubic closest-packed.
The lattice points in a cubic unit cell can be described in terms of a three-dimensional graph. Because all three cell-edge lengths are the same in a cubic unit cell, it doesn't matter what orientation is used for the a, b, and c axes. For the sake of argument, we'll define the a axis as the vertical axis of our coordinate system, as shown in the figure below.
Thinking about the unit cell as a three-dimensional graph allows us to describe the structure of a crystal with a remarkably small amount of information. We can specify the structure of cesium chloride, for example, with only four pieces of information.
- CsCl crystallizes in a cubic unit cell.
- The length of the unit cell edge is 0.4123 nm.
- There is a Cl- ion at the coordinates 0,0,0.
- There is a Cs+ ion at the coordinates 1/2,1/2,1/2.
NaCl should crystallize in a cubic closest-packed array of Cl- ions with Na+ ions in the octahedral holes between planes of Cl- ions. We can translate this information into a unit-cell model for NaCl by remembering that the face-centered cubic unit cell is the simplest repeating unit in a cubic closest-packed structure.
There are four unique positions in a face-centered cubic unit cell. These positions are defined by the coordinates: 0,0,0; 0,1/2,1/2; 1/2,0,1/2; and 1/2,1/2,0. The presence of an particle at one corner of the unit cell (0,0,0) requires the presence of an equivalent particle on each of the eight corners of the unit cell. Because the unit-cell edge connects equivalent points, the presence of a particle in the center of the bottom face (0,1/2,1/2) implies the presence of an equivalent particle in the center of the top face (1,1/2,1/2). Similarly, the presence of particles in the center of the 1/2,0,1/2 and 1/2,1/2,0 faces of the unit cell implies equivalent particles in the centers of the 1/2,1,1/2 and 1/2,1/2,1 faces.
The figure below shows that there is an octahedral hole in the center of a face-centered cubic unit cell, at the coordinates 1/2,1/2,1/2. Any particle at this point touches the particles in the centers of the six faces of the unit cell.
If Cl- ions occupy the lattice points of a face-centered cubic unit cell and all of the octahedral holes are filled with Na+ ions, we get the unit cell shown in the figure below.
- NaCl crystallizes in a cubic unit cell.
- The cell-edge length is 0.5641 nm.
- There are Cl- ions at the positions 0,0,0; 1/2,1/2,0; 1/2,0,1/2; and 0,1/2,1/2.
- There are Na+ ions at the positions 1/2,1/2,1/2; 1/2,0,0; 0,1/2,0; and 0,0,1/2.
ZnS crystallizes as cubic closest-packed array of S2- ions with Zn2+ ions in tetrahedral holes. The S2- ions in this crystal occupy the same positions as the Cl- ions in NaCl. The only difference between these crystals is the location of the positive ions. The figure below shows that the tetrahedral holes in a face-centered cubic unit cell are in the corners of the unit cell, at coordinates such as 1/4,1/4,1/4. An atom with these coordinates would touch the atom at this corner as well as the atoms in the centers of the three faces that form this corner. Although it is difficult to see without a three-dimensional model, the four atoms that surround this hole are arranged toward the corners of a tetrahedron.
- ZnS crystallizes in a cubic unit cell.
- The cell-edge length is 0.5411 nm.
- There are S2- ions at the positions 0,0,0; 1/2,1/2,0; 1/2,0,1/2; and 0,1/2,1/2.
- There are Zn2+ ions at the positions 1/4,1/4,1/4; 1/4,3/4,3/4; 3/4,1/4,3/4; and 3/4,3/4,1/4.
Read more at:
No comments:
Post a Comment