The structures of pure metals are easy to describe because the
atoms that form these metals can be thought of as identical
perfect spheres. The same can be said about the structure of the
rare gases (He, Ne, Ar, and so on) at very low temperatures.
These substances all crystallize in one of four basic structures:
simple cubic (SC), body-centered cubic (BCC),
hexagonal closest-packed (HCP), and cubic closest-packed (CCP).
When a solid crystallizes, the particles that form the solid pack as tightly as possible. To illustrate this principle, let's try to imagine the best way of packing spheres, such as ping-pong balls, into an empty box.
One approach involves carefully packing the ping-pong balls to form a square packed plane of spheres, as shown in the figure below.
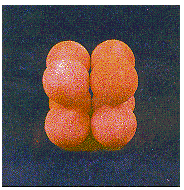This structure is called simple cubic packing. Each
sphere in this structure touches four identical spheres in the
same plane. It also touches one sphere in the plane above and one
in the plane below. Each atom in this structure can form bonds to
its six nearest neighbors. Each sphere is therefore said to have
a coordination number of 6.
A simple cubic structure is not an efficient way of using space. Only 52% of the available space is actually occupied by the spheres in a simple cubic structure. The rest is empty space. Because this structure is inefficient, only one element
poloniumcrystallizes
in a simple cubic structure.
Another approach starts by separating the spheres to form a square-packed plane in which they do not quite touch each other, as shown in the figure below.
This structure is called body-centered cubic because each sphere touches four spheres in the plane above and four more in the plane below, arranged toward the corners of a cube. Thus, the repeating unit in this structure is a cube of eight spheres with a ninth identical sphere in the center of the bodyin
other words, a body-centered cube, as shown in the figure below.
The coordination number in this structure is 8.
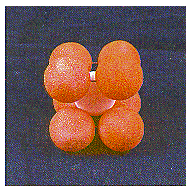
When a solid crystallizes, the particles that form the solid pack as tightly as possible. To illustrate this principle, let's try to imagine the best way of packing spheres, such as ping-pong balls, into an empty box.
One approach involves carefully packing the ping-pong balls to form a square packed plane of spheres, as shown in the figure below.
By tilting the box to one side, we can stack a second plane of spheres directly on top of the first. The result is a regular structure in which the simplest repeating unit is a cube of eight spheres, as shown in the figure below.
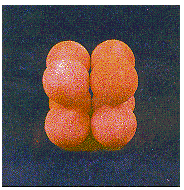
A simple cubic structure is not an efficient way of using space. Only 52% of the available space is actually occupied by the spheres in a simple cubic structure. The rest is empty space. Because this structure is inefficient, only one element
poloniumcrystallizes
in a simple cubic structure.Another approach starts by separating the spheres to form a square-packed plane in which they do not quite touch each other, as shown in the figure below.
The spheres in the second plane pack above the holes in the first plane, as shown in the figure below.
Spheres in the third plane pack above holes in the second plane. Spheres in the fourth plane pack above holes in the third plane, and so on. The result is a structure in which the odd-numbered planes of atoms are identical and the even-numbered planes are identical. This ABABABAB. . . repeating structure is known as body-centered cubic packing.
This structure is called body-centered cubic because each sphere touches four spheres in the plane above and four more in the plane below, arranged toward the corners of a cube. Thus, the repeating unit in this structure is a cube of eight spheres with a ninth identical sphere in the center of the body
in
other words, a body-centered cube, as shown in the figure below.
The coordination number in this structure is 8.
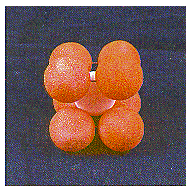
No comments:
Post a Comment