|
ATOMIC AND PHYSICAL PROPERTIES OF THE GROUP 2 ELEMENTS
This page explores the trends in some atomic and physical properties
of the Group 2 elements - beryllium, magnesium, calcium, strontium and
barium. You will find separate sections below covering the trends in
atomic radius, first ionisation energy, electronegativity and physical
properties. Even if you aren't currently interested in all these things, it would probably pay you to read most of this page. The same ideas tend to recur throughout the atomic properties, and you may find that earlier explanations help to you understand later ones. The physical properties are extremely difficult to explain, however, and you might not want to read about those unless you have to. Trends in Atomic Radius | |||||||
|
Note: You will find atomic radius covered in detail in another part of this site. If you choose to follow this link, use the BACK button on your browser to return quickly to this page. | |||||||
|
Explaining the increase in atomic radius The radius of an atom is governed by
| |||||||
|
Note: If you aren't sure about writing electronic structures using s and p notation it might be a good idea to follow this link before you go on. Use the BACK button on your browser to return quickly to this page. | |||||||
In each case, the two outer electrons feel a net pull of 2+ from the
nucleus. The positive charge on the nucleus is cut down by the
negativeness of the inner electrons.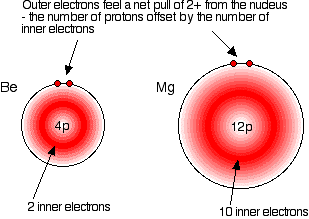 The only factor which is going to affect the size of the atom is therefore the number of layers of inner electrons which have to be fitted in around the atom. Obviously, the more layers of electrons you have, the more space they will take up - electrons repel each other. That means that the atoms are bound to get bigger as you go down the Group. | |||||||
|
Note: You may think that this is all a bit long-winded! It is, after all, fairly obvious that atoms will get bigger if you add more layers of electrons. Why, then, bother about exploring the net pull on the electrons from the centre of the atom? It is a matter of setting up good habits. If you are talking about atoms in the same Group, the net pull from the centre will always be the same - and you could ignore it without creating problems. That isn't true if you try to compare atoms from different parts of the Periodic Table. If you don't get into the habit of thinking about all the possible factors, you are going to make mistakes. | |||||||
|
Trends in First Ionisation Energy
First ionisation energy is the energy needed to remove the most
loosely held electron from each of one mole of gaseous atoms to make one
mole of singly charged gaseous ions - in other words, for 1 mole of
this process: | |||||||
|
Note: You will find ionisation energy covered in detail in another part of this site. If you choose to follow this link, use the BACK button on your browser to return quickly to this page. | |||||||
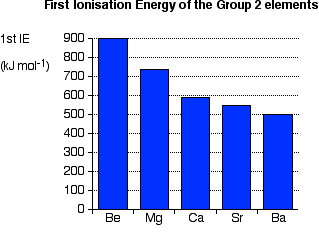 Explaining the decrease in first ionisation energy Ionisation energy is governed by
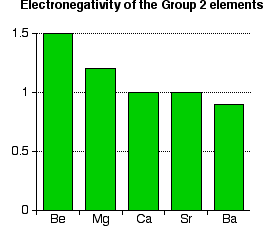
However, as you go down the Group, the distance between the nucleus and the outer electrons increases and so they become easier to remove - the ionisation energy falls. Trends in Electronegativity Electronegativity is a measure of the tendency of an atom to attract a bonding pair of electrons. It is usually measured on the Pauling scale, on which the most electronegative element (fluorine) is given an electronegativity of 4.0. | |||||||
|
Note: You will find electronegativity covered in detail in another part of this site. If you choose to follow this link, use the BACK button on your browser to return quickly to this page. | |||||||
 | |||||||
|
Note: You might argue that the fall doesn't apply throughout the Group because both calcium and strontium appear to have an electronegativity of 1.0. This is probably most easily explained by the fact that electronegativities are often only recorded to 1 decimal place. To two decimal places, calcium is 1.00 and strontium is 0.95. When these numbers are rounded to 1 decimal place, both would appear to have an electronegativity of 1.0. | |||||||
|
Explaining the decrease in electronegativity Imagine a bond between a magnesium atom and a chlorine atom. Think of it to start with as a covalent bond - a pair of shared electrons. The electron pair will be dragged towards the chlorine end because there is a much greater net pull from the chlorine nucleus than from the magnesium one. 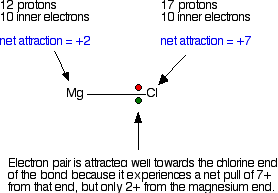 The large pull from the chlorine nucleus is why chlorine is much more electronegative than magnesium is. Now compare this with the beryllium-chlorine bond. The net pull from each end of the bond is the same as before, but you have to remember that the beryllium atom is smaller than a magnesium atom. That means that the electron pair is going to be closer to the net 2+ charge from the beryllium end, and so more strongly attracted to it.  Summarising the trend down the Group As the metal atoms get bigger, any bonding pair gets further and further away from the metal nucleus, and so is less strongly attracted towards it. In other words, as you go down the Group, the elements become less electronegative. As you go down the Group, the bonds formed between these elements and other things such as chlorine become more and more ionic. The bonding pair is increasingly attracted away from the Group 2 element towards the chlorine (or whatever). Trends in Melting Point, Boiling Point, and Atomisation Energy The facts Melting points 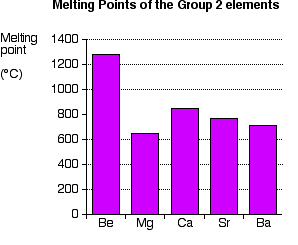 Boiling points 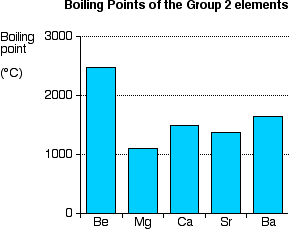 Atomisation energy This is the energy needed to produce 1 mole of separated atoms in the gas state starting from the element in its standard state (the state you would expect it to be in at approximately room temperature and pressure). 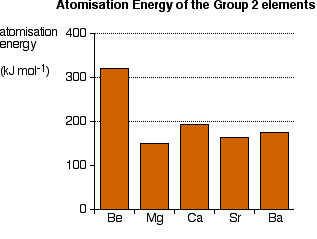 | |||||||
|
Warning! Unless you are doing a syllabus which expects you to be able to explain this, or unless your chemistry is good and you like a good argument, don't read on beyond this point. | |||||||
|
Trying to explain this The only explanations you are likely to ever come across relate to the melting points. I will give you the most common explanation, and then explain why I think it is completely wrong! The faulty explanation All of these elements are held together by metallic bonds. The melting points get lower as you go down the Group because the metallic bonds get weaker. The oddity of magnesium has to be explained separately. The atoms in a metal are held together by the attraction of the nuclei to the delocalised electrons. As the atoms get bigger, the nuclei get further away from these delocalised electrons, and so the attractions fall. That means that the atoms are more easily separated to make a liquid and finally a gas. As you go down the Group, the arrangement of the atoms in the various solid metals changes. Beryllium and magnesium are both hexagonal close-packed; calcium and strontium are face-centred cubic; barium is body-centred cubic. Don't worry if you don't know what this means. All that matters is that there is a change in crystal structure between magnesium and calcium. That is supposed to account for the fact that magnesium is out of line with the rest of the Group. Why I don't believe this explanation The odd position of magnesium Let's take this first, because that argument is relatively easy to demolish. Despite the fact that the first four elements have two different structures, those structures are both 12-co-ordinated. Each atom is touched by 12 surrounding atoms. In that case, you would expect the metallic bond to be similar in each case, because the orbitals are going to overlap and delocalise in the same sort of way. Any differences just due to the structures should only be minor. By contrast, barium is 8-co-ordinated (like the Group 1 metals). That's a less efficient packing, and you might expect that to be reflected in a much weaker metallic bond. Although the barium melting point is lower than that of strontium, it isn't dramatically lower. It just follows the general trend - suggesting that the major change of structure isn't making much difference. You can't have it both ways! If a minor change of structure at magnesium-calcium makes a huge difference, then a major one at barium should make an even bigger difference. It obviously doesn't. The strength of the metallic bonds Melting point isn't a good guide to the strength of the metallic bonds. When a metal melts, the bonds aren't completely broken - only loosened enough for the atoms to move around. Metallic bonds are still present in the molten metal, and aren't entirely broken until it boils. That means that boiling point, or the size of the atomisation energy, is a much better guide to the real strengths of the metallic bonds. With both of those measures, you are ending up with free atoms in the gas state with the metallic bond completely broken. Cotton and Wilkinson, in their classic degree level book Advanced Inorganic Chemistry say "The strength of binding between the atoms in metals can conveniently be measured by the energies of atomization of the metallic elements." (Third edition, page 68.) If you look back at the atomisation energy chart above, you will see that magnesium still has the lowest value, but there is no obvious trend in atomisation energies as you go down the Group. The explanation about weaker metallic bonds as you go down the Group can't be accurate either. If you look at figures for Group 1 rather than Group 2, then the trends for all the various measures (melting point, boiling point and atomisation energy) work almost perfectly as you go down the Group. There is obviously something happening in Group 2 which is causing the problem. I have no idea at all what it might be. A final comment I have had a request for solid information about this on Chemguide since 2002, during which time this page will have been read by hundreds of thousands, if not millions, of visitors. In all that time, nobody has suggested an explanation which would account for the low melting point value for magnesium, or the lack of any pattern with the other two properties. If you can see flaws in what I have said above, please get in touch with me. I would also be grateful to anyone who could point me towards an explanation, even if it is too difficult to use at this level, or even too difficult for me to understand. But that explanation has to be capable of accounting for all the variations in the data. There is one book that I have come across which is honest enough to admit the difficulty. A.G.Sharpe, in his degree level book Inorganic Chemistry admits that there is no easy explanation for the variations in the physical data in Group 2. If that is indeed the case, as looks pretty likely, it is a pity that anyone should encourage faulty explanations like the one above. Much better to have no explanation than a deeply flawed one. | |||||||
Saturday, 29 June 2013
ATOMIC AND PHYSICAL PROPERTIES OF THE GROUP 2 ELEMENTS
Labels:
Inorganic Chemistry
Subscribe to:
Post Comments (Atom)
No comments:
Post a Comment